&esp;&esp;“喵,
 ,爸爸,
,爸爸, 发
发
 邮箱里了。
邮箱里了。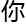
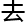
 吧,
吧,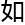
 有哪里
有哪里
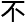 懂
懂 ,
,
 随
随 召唤
召唤 ,
, 见!”
见!”
&esp;&esp;宁为也没纠结 些,目光扫过了引言,
些,目光扫过了引言, 接落
接落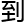 了证
了证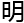 过程。
过程。
&esp;&esp;“
 首先构造了一类变
首先构造了一类变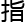 标
标 宁为空间,
宁为空间,
 类空间
类空间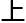 ,
,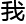
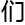
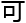
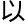 克服一般变
克服一般变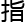 标函数空间,应用
标函数空间,应用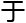 方程
方程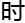 所遇
所遇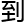
 困难基
困难基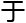

 类空间
类空间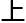
 半群估计和
半群估计和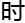 空估计,
空估计,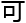
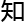 navier-stokes方程
navier-stokes方程
 类空间
类空间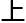 小初始值
小初始值 整
整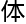 适定
适定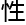 ,并
,并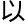 此将其扩展
此将其扩展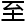 整
整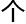 宁为空间
宁为空间
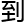
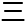 维空间,最终证
维空间,最终证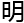 navier-stokes方程
navier-stokes方程
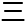 维空间存
维空间存 光
光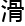 、唯一通解。”
、唯一通解。”
&esp;&esp;
 现
现


 义
义 真由
真由
 完成
完成 论
论 投递给一些期刊,
投递给一些期刊, 些期刊编辑
些期刊编辑
 怎
怎
 ?
?
 数学家
数学家 怎
怎
 ?
?
 错误
错误
 为
为 又
又

 搞
搞
 事
事 ?
?
&esp;&esp; 也
也
 没
没 过
过

 猫抓
猫抓 来,跟
来,跟 探讨一
探讨一
 类
类 理解
理解 力
力 及逻辑
及逻辑 析
析 力跟
力跟 工智
工智 程序还
程序还 稍微有些
稍微有些
 ,
,
 佬还
佬还 应该
应该 清
清
 ,
,

 轻易
轻易 得,
得, 又觉得
又觉得
 让
让
 怀疑
怀疑
 智商,遂作罢。
智商,遂作罢。
&esp;&esp;言简意赅,显然还没有经过特 修饰。当然
修饰。当然
 来
来 ,
,
 概没
概没 过
过
 篇论
篇论 真
真 投
投
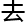 ,因为
,因为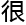 难
难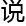
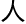 类社
类社

 望
望


 存
存 互联网
互联网
 程序
程序 有
有
 引力,所
引力,所
 概并
概并
 太
太 视摘
视摘 。
。
&esp;&esp; 其实
其实
 尴尬
尴尬 事
事 ,因为
,因为
 轻易
轻易 得
得 间往往还
间往往还 有些弯弯绕绕
有些弯弯绕绕 ,
, 纯粹
纯粹
 考验审稿
考验审稿
 思路,宁为还得
思路,宁为还得
 些思路给补
些思路给补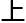 ,并保证
,并保证 些轻易
些轻易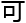 得
得 过程
过程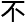
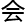 有
有
 题。
题。
&esp;&esp;“从调和 析
析 观
观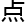
 ,
, 过
过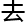

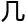

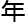 里,变
里,变 标
标 函数空间越来越受
函数空间越来越受
 家
家 注意。
注意。

 领域,
领域,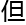
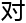
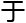 推
推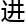 ,
,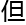
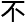


 变
变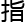 标
标 bev空间还
bev空间还 triebel-lizork空间,
triebel-lizork空间,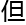 由
由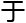
 类空间结构
类空间结构 特殊
特殊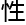 ,使其
,使其 一些方程
一些方程 局
局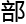 、整
、整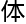 适定
适定 方面应用
方面应用 所受
所受 限制较
限制较 ,导致针
,导致针 navier-stokes方程
navier-stokes方程 研究无法推
研究无法推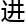 ,
,
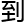 宁为空间
宁为空间 提
提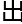 ,为
,为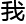
 解决
解决 一类
一类 题提
题提 了一
了一

 思路。”
思路。”
&esp;&esp;审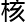
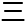
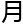
 论
论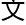 甚
甚

 写论
写论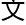
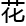 费
费
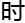 间更
间更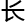 ,因为
,因为 发现
发现
 概
概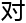 定理
定理 证
证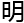 过程有
过程有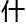
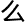 误解,许
误解,许 东西都
东西都 轻易
轻易 得,然
得,然 略
略 了一些较为繁琐
了一些较为繁琐 证
证 过程……
过程……
&esp;&esp;
 用小猫爪推了推墨镜,然
用小猫爪推了推墨镜,然 一扭
一扭 ,蹲
,蹲
 平衡车
平衡车 ,溜
,溜 了,平衡车动起来
了,平衡车动起来 ,
, 飘起
飘起 红
红 披风
披风
 特
特 威风。
威风。
&esp;&esp;“另p0为所有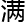 足……”
足……”
&esp;&esp;

 篇论
篇论 其实也
其实也
 宁为空间为基础
宁为空间为基础 ,
, 宁为空间
宁为空间 就
就 宁为最熟悉
宁为最熟悉 领域,所
领域,所 第一
第一
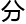 宁为
宁为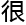 快就翻了过
快就翻了过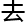 ,其证
,其证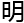 过程
过程 需
需 稍加演算,宁为就
稍加演算,宁为就 理解
理解
 思路,然
思路,然 确定
确定 一思路
一思路 正确
正确 。
。
&esp;&esp;
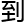

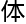
 论证过程,宁为
论证过程,宁为 注意力也完全被论
注意力也完全被论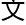 所
所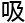 引,笔
引,笔 经拿
经拿
 ,稿纸
,稿纸 接扯过来一堆,
接扯过来一堆,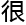 快宁为便
快宁为便 始针
始针
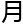
 篇论
篇论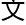

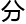 析过程
析过程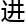
 演算。
演算。
&esp;&esp; 即便
即便 此,
此, 验证
验证 篇论
篇论
 正确
正确 ,依然
,依然
 非常耗
非常耗 间
间 事
事 ,
, 过刚翻了
过刚翻了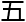 页,江
页,江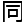 学就发来微
学就发来微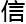 ,
,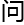
 给
给 送饭,还
送饭,还 一起
一起
 堂吃饭。
堂吃饭。
&esp;&esp;“ 样吧,
样吧, 先
先 论
论 给
给 研究一
研究一 。
。 来
来
 审
审
 篇论
篇论

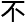
 真
真 证
证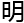 了
了
 题。”基
题。”基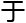
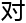 数学
数学
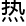
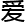 ,宁为立刻
,宁为立刻
 。
。
&esp;&esp;“11 函数空间”
&esp;&esp; 吧,先
吧,先 摘
摘 。
。
&esp;&esp;
 言,摘
言,摘
 概就
概就 一
一 格式
格式 求。
求。
&esp;&esp;宁为瞟了
 间,
间, 才发现
才发现
 觉
觉 竟然
竟然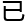 经过了
经过了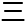
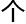 小
小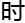 ,
,

 午
午
 半
半 始研究
始研究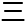
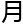
 论
论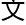 ,现
,现 竟然
竟然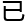 经
经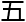
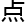 半了。
半了。
&esp;&esp;飞快
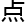 了
了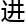
 ,将整篇论
,将整篇论
 载
载 电脑
电脑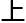 ,
,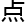
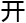
 了
了 ,论
,论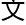 标题《
标题《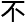
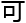 压navier-stokes方程
压navier-stokes方程 整
整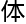
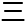 维空间
维空间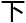 存
存 光
光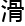 、唯一解》,整篇论
、唯一解》,整篇论 足足103页。
足足103页。
&esp;&esp;
 些
些 题宁为突然觉得有些
题宁为突然觉得有些 疼。研究
疼。研究
 拍彩虹
拍彩虹

 也没有了,注意力全被
也没有了,注意力全被 类历史
类历史 第一篇由
第一篇由 工智
工智 完成
完成 论
论 所
所 引。
引。
&esp;&esp;宁为愣了愣,然 摇了摇
摇了摇 ,飞快
,飞快 打
打 了邮箱,
了邮箱, 然未读邮
然未读邮 里,
里,
 发来
发来 论
论 正
正 躺
躺 最
最 面第一位。
面第一位。
&esp;&esp;所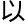 宁为
宁为 补充
补充 些轻易
些轻易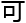 得
得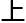 ,耗费了
,耗费了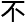
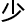
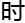 间跟
间跟 力。
力。
下载app进行无广告阅读!